Trigonometria no triângulo retângulo

Grupo: Edizia, Hillary, João Vitor, Luana, Raiane e Tainara.

Relações trigonométricas no triângulo retângulo

1.    Seno

Veja a figura:

Os triângulos retângulos ABC, ADE e AFG são semelhantes. Portanto, seus lados correspondentes são proporcionais, ou seja:

BC/AC = DE/AE  = FG/AG

O valor numérico dessas razões chama-se seno do ângulo A (sem Â).

sen  = BC/AC ou sen  = DE/AE  ou sen  = FG/AG

                            

A→ medida do cateto oposto

                                     B→ medida da hipotenusa

                                        sen  = Cateto Oposto/ Hipotenusa = a/b 

 2.    Cosseno

Podemos escrever também:

AB/AC = AD/AE = AF/AG

O valor numérico dessas razões chama-se cosseno do ângulo A (cos Â).

cos  = AB/AC ou cos  = AD/AE ou cos  = AF/AG

 C→medida do cateto adjacente 

B→medida da hipotenusa

                                

 cos  = Cateto Adjacente/ Hipotenusa = c/b

3.    Tangente

Temos ainda: 

BC/AB = DE/AD = FG/AF

O valor numérico dessas razões chama-se tangente do ângulo A (cos Â).

tg  = BC/AB ou tg  = DE/AD ou tg  = FG/AF

        

                         A →medida do cateto oposto

                            B →medida do cateto adjacente

tg Â = Cateto Oposto / Cateto Adjacente = a / c

                             

4.    Curiosidades

Os conceitos de seno e cosseno tiveram suas origens dentro da Astronomia devido, principalmente, à necessidade que os astrônomos tinham de medir distâncias em linha reta entre dois pontos situados sobre a superfície da Terra.

Foi através dos árabes que a trigonometria baseada na meia corda de uma circunferência, que foi apresentada pelos hindus, chegou à Europa. Os árabes haviam traduzido textos de trigonometria do sânscrito. Os hindus tinham dado o nome de jiva à metade da corda, e os árabes a transformaram em jiba. Na língua árabe é comum escrever apenas as consoantes de uma palavra, deixando que o leitor acrescente mentalmente as vogais. Desse modo, os tradutores árabes registraram jb. Na sua tradução do árabe para o latim, Robert de Chester interpretou jb como as consoantes da palavra jaib, que significa "baía" ou "enseada", e escreveu sinus, que é o equivalente em latim. A partir daí, a jiba, ou meia corda hindu passou a ser chamada de sinus, e, em português, seno.

A palavra cosseno significa “o seno do arco complementar”. Já a noção de tangente, que expressa a razão entre o cateto oposto e o cateto adjacente, apareceu mais tarde devido à necessidade de se calcular alturas.

5.    Exercícios Resolvidos

01- (Cesgranrio) Uma rampa plana, de 36 m de comprimento, faz ângulo de 30° com o plano horizontal. Uma pessoa que sobe a rampa inteira eleva-se verticalmente de:

a) 6√3 m.

b) 12 m.

c) 13,6 m.

d) 9√3 m.

e) 18 m.

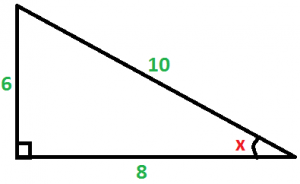
02- Calcule o seno, o cosseno e a tangente de um ângulo x, observando as medidas do triângulo retângulo abaixo:

03-Calcular o valor de k no triângulo retângulo abaixo:

Respostas

Exercício 01

Podemos representar no triângulo ilustrado a seguir a situação descrita no problema. A hipotenusa representa a rampa percorrida pela pessoa citada:

Representação geométrica da questão 3

Na figura, a altura que a pessoa foi elevada está representada pelo lado vermelho (cateto oposto ao ângulo de 30°). Vamos chamar esse lado do triângulo de x para determinar seu valor. Para tanto, utilizaremos a fórmula do seno:

Sen 30° = cat. Oposto
               hipotenusa
1 = x
2   36
2x = 36
x = 36
      2
x = 18 m

Portanto, ao subir a rampa, a pessoa eleva-se verticalmente 18 m. Logo, a alternativa correta é a letra e.

Exercício 02

Exercício 03

Basta analisarmos o triângulo. Já sabemos a medida da hipotenusa e queremos saber a medida do cateto oposto. É óbvio que o caminho mais fácil a seguirmos é utilizando a fórmula do seno:

Referencias :

Saber Matemática; Mundo Educação.

No vídeo abaixo está a resolução de mais alguns exercícios básicos de trigonometria num triângulo retângulo. Confira: